
Un système modélisé par un point matériel possède de l'énergie cinétique dès lors qu'il est en mouvement dans un référentiel donné.
La formule
Dans un référentiel où le système, de masse m, a une vitesse de norme v, son énergie cinétique est :
\( \displaystyle\mathsfit {E_c = \tfrac{\mathsf{1}}{\mathsf{2}}mv^\mathsf{2}}\)
\( \displaystyle\mathsf {\mathsfit{E_c}\ en\ \textnormal{joules}\ (J)}\)
\( \displaystyle\mathsf {\mathsfit{m}\ en\ \textnormal{kilogrammes}\ (kg)}\)
\( \displaystyle\mathsf {\mathsfit{v}\ en\ m.s^{-1}}\)
Rappel :
Si l'énergie cinétique est stockée par le système, le travail est une énergie de transfert entre le milieu extérieur et le système.
Le travail de A à B de la force F constante est le produit scalaire de cette force par le vecteur déplacement AB :
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}\ =\ \overrightarrow {\mathsfit F}.\overrightarrow {\mathsf {AB}}\ =\ \mathsfit F.\mathsf {AB}.cos\ α}\)
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}\ en\ joules\ (J)}\)
\( \displaystyle\mathsf {\mathsfit {F}\ en\ newtons\ (N)}\)
\( \displaystyle\mathsf {\mathsf {AB}\ en\ mètres\ (m)}\)
cos α > 0
\( \mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}\ >\ 0}\)
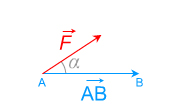
effet moteur
le système gagne en énergie
cos α = 0
\( \mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}\ =\ 0}\)
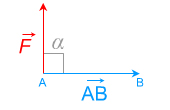
effet nul
l'énergie transférée est nulle
cos α < 0
\( \mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}\ <\ 0}\)
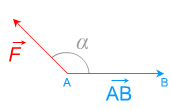
effet résistant
le système perd de l'énergie
Remarque : Dans un repère orthonormé (O;i, j), le produit scalaire de u(x,y) et v(x',y') est (xx' + yy').
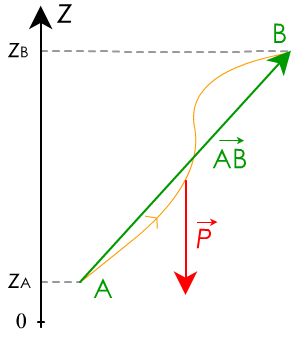
Le travail du poids est donc : \( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}\ =\ \overrightarrow {\mathsfit P}.\overrightarrow {\mathsf {AB}}\ =\ \mathsfit P.\mathsf {AB}.cos\ α}\) (voir doc 1), mais :
- dans un repère muni d'un axe Oz orienté vers le haut,
- parce que P est vertical et que \( \displaystyle\mathsf {cos\ α\ =\ \frac{z_A\ -\ z_B}{AB}}\),
- en simplifiant par AB, il vient : \( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}\ =\ \mathsfit P.\mathsf {(}{z_\mathsf A}-z_{\mathsf B}\mathsf {)}}\)
Lorsque un système de masse m se déplace d’un point A d’altitude zA à un point B d’altitude zB, le travail de son poids P vaut :
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}\ =\ \mathsfit m.g.\mathsf {(}{z_\mathsf A}-z_{\mathsf B}\mathsf {)}}\)
\( \displaystyle\mathsf {\mathsfit {W}\ en\ joules\ (J)}\)
\( \displaystyle\mathsf {\mathsfit {m}\ en\ kilogrammes\ (kg)}\)
\( \displaystyle\mathsf {\mathsfit {z}\ en\ mètres\ (m)}\)
g = 9,81 N.kg-1 est la norme du champ de pesanteur.
zA > zB :
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}}\) est un nombre positif.
Sur le trajet AB, le système a reçu de l'énergie.
Sur ce trajet, le travail du poids est globalement moteur.
zA = zB :
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}}\) est nul.
Sur le trajet AB, le système a reçu autant d'énergie qu'il en a perdu.
Sur ce trajet, le travail du poids est globalement nul.
zA < zB :
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}}\) est un nombre négatif.
Sur le trajet AB, le système a perdu de l'énergie.
Sur ce trajet, le travail du poids aura été globalement résistant.
doc 1 \( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}\ =\ \mathsfit m.g.\mathsf {(}{z_\mathsf A}-z_{\mathsf B}\mathsf {)}}\)
le trajet est quelconque...
le système descend : W > 0
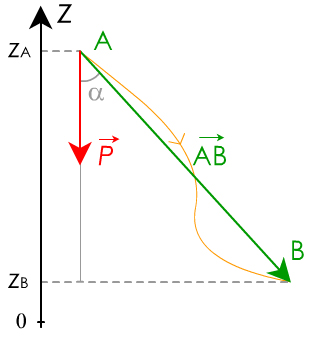
doc 2 \( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {P}\mathsf {)}}\ =\ \mathsfit m.g.\mathsf {(}{z_\mathsf A}-z_{\mathsf B}\mathsf {)}}\)
le trajet est quelconque...
le système monte : W < 0
Exercice : Un colis de 5,0 kg est lâché sans vitesse initiale d’un point A (zA = 2,0 m) jusqu’au sol horizontal (zsol = 0 m) en suivant deux trajets possibles :
Trajet 1 : chute verticale ;
Trajet 2 : glissement le long d’une planche de longueur 4 m qui part du même point A et arrive aussi au sol.
1. Calculer le travail du poids dans le premier cas.
2. Quel est le travail du poids dans le second cas ?
Donnée : On prendra g = 9,81 N/kg
Les frottements f subis par un système en mouvement sont parallèles au déplacement, et de sens opposé. α = 180° et donc cos α = -1.
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {f}\mathsf {)}}\ =\ -\mathsfit f.\mathsf {AB}}\)
\( \displaystyle\mathsf {\mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {f}\mathsf {)}}\ en\ joules\ (J)}\)
\( \displaystyle\mathsf {\mathsfit {f}\ en\ newtons\ (N)}\)
\( \displaystyle\mathsf {\mathsf {AB}\ en\ mètres\ (m)}\)
W < 0 : les frottements sont résistants
Exercice : Dans l'exercice précédent, une force de frottement f, de 22 N, s'exerce entre le carton et la planche de 4,0 m.
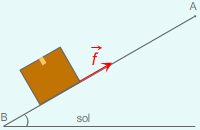
Calculer le travail de cette force de frottement.
L'énergie transférée au système par travail de toutes les forces appliquées aura une influence sur son énergie cinétique.
Dans un référentiel galiléenRéférentiel dans lequel le principe d'inertie est vérifié. Le référentiel terrestre sera considéré comme galiléen, la variation d'énergie cinétique ΔEc d'un systèmemodélisé par un point matériel, de masse m entre deux points A et B est la somme des travaux des forces qu’il subit.
\( \displaystyle\mathsf {\mathsfit {\mathsf {Δ}{\mathsfit {E_c}}\ =\ \sum \mathsfit {W_{\mathsf {AB}}\mathsf {(}\overrightarrow {F}\mathsf {)}}}}\)
Exercice : Quelle sera la vitesse du colis de 5,0 kg de l'exercice précédent lorsqu'il atteint le sol après avoir glissé sur la planche ?