
La spectrophotométrie et le dosage par titrage avec suivi colorimétrique (le suivi conductimétrique n'est pas vu ici).
Ces deux techniques permettent de déterminer la concentration d'une solution.
Dans les deux cas, la couleur intervient.
1.1. Absorbance :
Une solution absorbe certaines radiations et en laisse passer d'autres. Les radiations qui ne sont pas absorbées donnent sa couleur à la solution. Cette couleur dépend de la concentration.
L'absorbance Aλ mesure la capacité d'une solution à absorber la lumière à une longueur d'onde donnée.
Cette grandeur n'a pas d'unité.
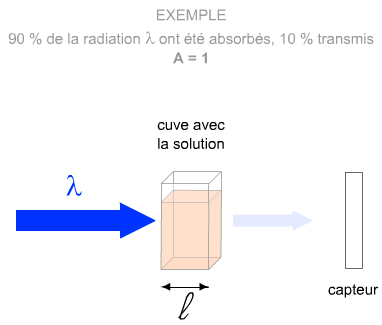
Si Aλ = 0 → 100 % transmis.
Si Aλ = 1 → 10 % transmis.
Si Aλ = 2 → 1 % transmis.
Si Aλ = 3 → 0,1 % transmis ; (aucune formule en 1e).
1.2. Spectre d'absorption :
Un spectre d'absorption est une courbe. Elle représente la variation de l'absorbance en fonction de la longueur d'onde.
Aλ = f(λ)
Lien entre la couleur de la solution et son spectre.
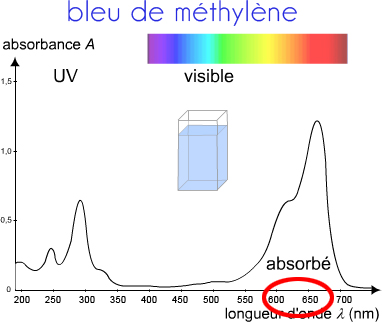
Exemple du bleu de méthylène.
En lumière blanche, avec toutes les radiations du spectre visible, la solution est bleue.
Le spectre nous dit que les radiations des zones rouge et orangé sont absorbées par cette solution. Nous voyons ce qui n'a pas été absorbé.
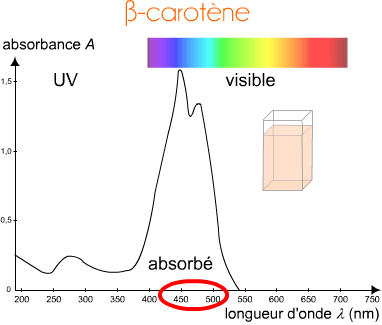
Exemple du bêta-carotène.
En lumière blanche, avec toutes les radiations du spectre visible, la solution est orangée.
Le spectre nous dit que les radiations des zones allant du violet au vert sont absorbées. Nous voyons la "somme" des radiations du jaune au rouge.
Dosage par étalonnage.
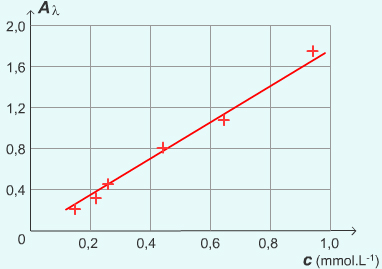
Exercice : Déterminer une concentration à partir d'une courbe d'étalonnage.
La courbe ci-contre donne les mesures d'absorbances d'une solution de diiode pour diverses concentrations, pour une longueur d'onde fixe (λ = 475 nm).
On réalise la spectrophotométrie UV-visible dans les mêmes conditions, pour une solution de diiode de concentration inconnue.
Le spectrophotomètre donne une absorbance A = 1,4 pour λ = 475 nm.
Trouver la concentration de la solution étudiée.
1.3. Loi de Beer-Lambert :
La droite d'étalonnage de l'exercice précédent est une représentation de la loi de Beer-Lambert :
L'absorbance Aλ d'une solution, contenant un soluté absorbant la longueur d'onde λ, est proportionnelle à la concentration c de ce soluté et à la longueur \( \displaystyle\mathsfit{\ell} \) de solution traversée.
La lettre ε (epsilon) est le coefficient d'extinction molaire. ε dépend de λ et de l'espèce colorée.
\( \displaystyle\mathsfit{A_\lambda =\ {\epsilon} \times {\ell} \times {c}} \)
\( {\displaystyle\mathsfit{A_\lambda}\ \mathsf {sans\ unité}} \)
\( {\displaystyle\mathsfit{\epsilon}\ \mathsf{(L.mol^{-1}.cm^{-1})}} \)
\( {\displaystyle\mathsfit{\ell}\ \mathsf{(cm)}} \)
\( {\displaystyle\mathsfit{c}\ \mathsf{(mol.L^{-1})}} \)
Exercice : La loi de Beer-Lambert peut s'écrire \( \displaystyle\mathsfit{A =\ {k} \times {c}} \) (avec \( \displaystyle\mathsf{k =\ {\epsilon} \times {\ell}} \))
La courbe de l'exercice précédent a été réalisée avec des cuves de spectrophotomètre UV-visible de largeur \( {\displaystyle\mathsfit{\ell}\ =\ \mathsf{1,0\ cm}} \).
Q. Trouver ε de la solution étudiée.
2.1. Principe
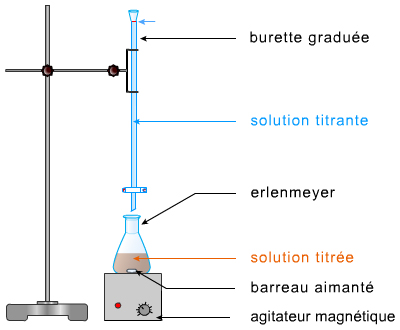
Protocole
1. Préparation des solutions :
─ On verse un volume V de solution (c = ?) contenant l'espèce à titrer (erlenmeyer).
─ Cette espèce réagit avec une autre de concentration connue, le réactif titrant (burette).
2. Réaction chimique :
─ Dans ce cours, c'est une réaction d'oxydoréduction.
─ Elle doit être totale (un réactif disparaît : limitant)
3. Ajout du titrant :
─ On ajoute progressivement le réactif titrant jusqu'à un changement de couleur.
─ Cette situation se nomme l'équivalence
montage ↓
2.2. L'équivalence
Que se passe-t-il dans l'erlenmeyer ?
1. Au début de la réaction :
─ Le réactif titré (présent dans l'erlenmeyer) est en excès.
─ Le réactif titrant est le réactif limitant (ajouté goutte à goutte, il disparaît).
2. À l'équivalence :
─ Les quantités ont alors réagi dans les proportions stœchiométriques.
─ À ce point précis, il n'y a plus de réactif limitant, car les deux réactifs ont réagi entièrement.
3. Après :
─ Après le point d'équivalence, c'est l'inverse : le réactif titré devient limitant.
─ Quand on ajoute le réactif titrant, il s’accumule dans l’erlenmeyer sans réagir.
Il y a un changement de réactif limitant au point d'équivalence, marquant le passage d'une limitation par le réactif titrant à une limitation par le réactif titré.
2.3. Deux exemples et un exercice
Exemple 1 : l'iodométrie
On utilise souvent l'ion thiosulfate S2O32- pour titrer I2.
La couleur jaune-brun, ici, est portée par I2.
Couples rédox : S4O62-/S2O32- et I2(aq)/I-
Pour être raccord avec le gif 2, l'équation aA + bB = ... s'écrirait :
2 S2O32-(aq) + I2(aq) = ...
\( \displaystyle\mathsf{\frac{\mathsfit{n}_{S_2O_3^{2-}(éq)}}{2}\ =\ \frac{\color{RedOrange}\mathsfit{n}_{I_2(t=0)}}{1}}\)
Remarque : les lettres A et B peuvent être inversées ailleurs, sur d'autres documents.
Exemple 2 : manganimétrie
On utilise l'ion permanganate MnO4-, pour titrer des réducteurs.
Le couple MnO4-/Mn2+ est en jeu, en milieu acide. Mn2+ est stable.
Exemple de couples : MnO4-/Mn2+ et Fe3+/Fe2+
Pour être raccord avec le gif 3, l'équation aA + bB = ... s'écrirait :
MnO4- + 5 Fe2+ +... = ...
\( \displaystyle\mathsf{\frac{\color{purple}\mathsfit{n}_{MnO_4^{-}(éq)}}{1}\ =\ \frac{\mathsfit{n}_{Fe^{2+}(t=0)}}{5}}\)
Exercice : Un volume V de 25,0 mL d'une solution acidifiée de sel de Mohr, contenant des ions fer II (Fe2+) a été titré avec Véq = 20,0 mL de permanganate de potassium (KMnO4) de concentration cMn04- = 0,020 mol.L-1.
Quelle est la concentration en ions Fe2+ de la solution de sel de Mohr ?
Les couples rédox : MnO4-(aq)/Mn2+(aq) et Fe3+(aq)/Fe2+(aq)