Contrairement aux solides, les fluides ne conservent pas de forme fixe mais adoptent celle du récipient qui les contient.
- à l'état liquide, les entités sont mobiles, désordonnées, proches. Un liquide a un volume propre.
- à l'état gazeux, les entités sont espacées, désordonnées, agitées, occupent tout l'espace offert.
1.1. Masse volumique
La masse volumique est le quotient entre la masse m de matière et le volume V occupé par cette matière :
\( \displaystyle\mathsfit {\rho = \frac{m}{V}} \)
\( \displaystyle\mathsf {m\ (kg)} \)
\( \displaystyle\mathsf {V\ (m^3)} \)
\( \displaystyle\mathsf {\rho\ (kg.m^{-3})} \)
Comportement microscopique des entités
Deux paramètres influencent la valeur d'une masse volumique :
- La masse de chaque entité (molécule...) ;
- L'espacement de ces entités, soit leur nombre pour un volume donné. Ce 2e paramètre influence tous les fluides mais plus les gaz du fait de l'éloignement des entités dans cet état.
Les unités données avec la formule sont les USI (Unités du Système International). Une masse volumique peut être donnée en g/cm3 ou en g/L.
doc 1. Conversions utiles
1 g/cm3 = 1000 kg/m3
1 kg/L = 1000 kg/m3
1 g/L = 1kg/m3
1.2. Pression
La pression dans un fluide au repos se mesure à l'aide d'un pressiomètre (ou manomètre). Le symbole est P et l'unité le pascal (Pa).
Comportement microscopique des entités
La pression dans un fluide au repos est le résultat des collisions entre les particules qui le constitue.
Dans un fluide, les molécules sont en mouvement constant et subissent des collisions avec leurs voisines dans toutes les directions, échangeant leur énergie.
Analogie : imaginer une foule dense dans un concert, où chaque individu subit la "pression" des personnes autour de lui.
doc 2. modèle d'un fluide "au repos" (gaz)
collisions des molécules, entre elles et sur les parois
1.3. Température
La température dans un fluide au repos se mesure à l'aide d'une sonde thermométrique. Le symbole est T et l'unité le degré Kelvin (K).
T (K) = T (°C) + 273,15 (utile pour la loi des gaz parfaits vue en Terminale 😏 doc 3)
Comportement microscopique des entités
La température d’un fluide au repos traduit le niveau d’agitation microscopique des particules (molécules ou atomes) qui le composent. Si T augmente, la vitesse (et donc l'énergie cinétique) des particules augmente.
doc 3. Sur le zéro absolu et l'échelle Kelvin
À température constante, la pression P d'une quantité donnée de gaz varie en fonction de son volume V suivant la loi de Mariotte :
\( \displaystyle\mathsfit {P.V = constante} \)
doc 4. modèle de comportement d’un gaz
loi de Mariotte
Exercice : Le piston d'une seringue sans liquide est en équilibre, sans contrainte (doc 4). Le manomètre indique 1012 hPa (prononcer hectopascal). Le volume intérieur est de 50 mL.
Que vaut la pression lorsqu'on réduit le volume à 25 mL ?
Les collisions sur une paroi des entités constituant un fluide entrainent une action mécanique pouvant se modéliser par une force pressante (doc 5).
Un fluide à la pression P est en contact avec une paroi plane d'aire S.
\( \displaystyle\mathsfit {F =\ P.S} \)
F (N)
P (Pa)
S (m²)
et donc : \( \displaystyle\mathsfit {P = \frac{F}{S}} \)
et : \( \displaystyle\mathsfit {S = \frac{F}{P}} \)
doc 5. force pressante
sur une paroi plane
Exercice : Un petit sous-marin d’exploration descend à une profondeur de 200 mètres sous la surface de la mer. À cette profondeur, la pression de l’eau est d’environ 2,02 MPa (mégapascals). La vitre avant du sous-marin est circulaire et a un diamètre D = 30 cm.
Quelle est la valeur de la force pressante exercée sur ce hublot ?
Données :
π ≈ 3,14
1 MPa = 106 Pa
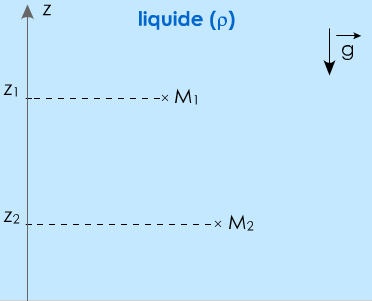
La loi énoncée ici ne s'applique qu'aux fluides incompressibles au repos. Nous nous limiterons donc aux liquides.
Soient M1 et M2 deux points dans un liquide, d’altitudes respectives z1 et z2, où règnent les pressions respectives P1 et P2.
La loi fondamentale de la statique des fluides incompressibles dit :
P2 − P1 = ρ g (z1− z2 )
P (Pa)
ρ (kg.m3)
z (m)
g = 9,81 N.kg-1
⚠️ La pression est une grandeur scalaire. La position z est orientée. La formule donnée sera utilisée avec un axe Oz dirigé vers le haut (doc 6). Pour un axe orienté vers le bas, on utilise :
P2 − P1 = ρ g (z2− z1 )
Retenons que la différence de pression ΔP est proportionnelle à |Δz| 😏.
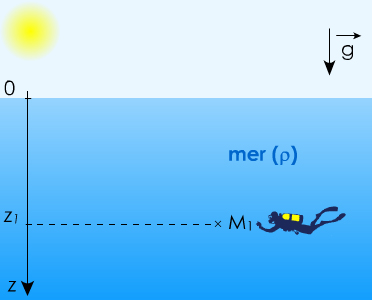
Exercice : Un plongeur descend à 10 mètres sous la surface de la mer. Quelle est la pression à cette profondeur ?
Données :
g = 9,81 N.kg-1
Masse volumique de l'eau de mer : ρ = 1025 kg.m-3
Patm (pression de l'eau à la surface) : P0 = 1,0.105 Pa
Pression relative : Un pneu gonflé à 2,5 bars est à 2,5 bars au-dessus de l’air ambiant.
doc. 6 loi fondamentale de la statique des fluides
⚠️ axe vers le haut
doc. 7 plongée sous-marine
⚠️ axe vers le bas