1.1. Électrisation
Thalès (∼ 600 av. J.-C.) a été le premier à parler de l'ambre (ἤλεκτρονélectron
😮) frottée pouvant attirer de petits objets légers comme des brins de paille.
Contact
L’électrisation par contact est un transfert d’électrons d’un corps vers un autre.
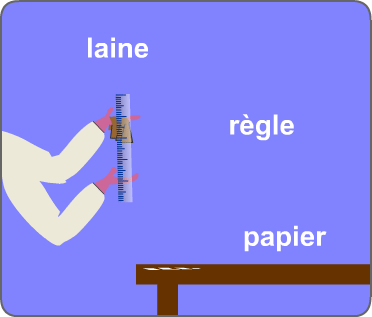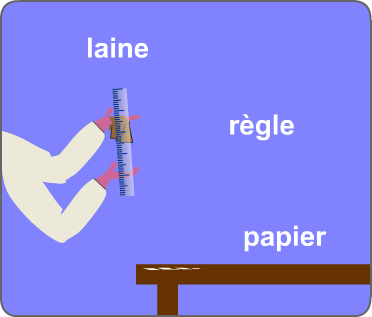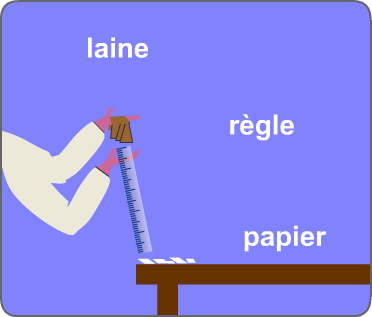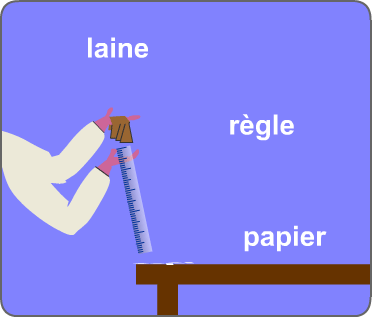
Exemple : Lors du frottement d'une règle en plastique (matière isolante) avec de la laine, la règle arrache des électrons au tissu (doc 1). L'excès d'électrons donne une charge négative à la règle.
Influence
La règle frottée peut attirer des objets légers (doc 1). Les charges ne quittent pas le papier, mais elles se déplacent sous l'influence de la règle proche.
À l'approche d'un objet électrisé, sans contact, les charges électriques d'un autre objet se déplacent. C'est l’électrisation par influence.
doc 1. électrisation par contact puis...
...par influence
1.2. Loi de Coulomb
Un point matérielobjet réel modélisé par un point A, portant une charge électrique qA exerce sur B, de charge qB, éloignée d'une distance d, une force :
\( \displaystyle\mathsf {\overrightarrow{F}_{_{A/B}}\ =\ k\ \frac{q_A.q_B}{d^2}\ \overrightarrow{u}_AB} \)
\( \displaystyle\mathsf {F\ (N)} \)
\( \displaystyle\mathsf {q\ en\ coulomb\ (C)} \)
\( \displaystyle\mathsf {d\ (m)} \)
\( \displaystyle\mathsf {k\ =\ 9,0.10^9\ N.m^2.C^{-2}} \)
La 3e loi de Newton donne : \( \displaystyle\mathsf {\overrightarrow{F}_{_{A/B}}\ =-\ \overrightarrow{F}_{_{B/A}}} \)
Une charge q porte le signe ⊕ ou le signe ⊖. Dès lors, si :
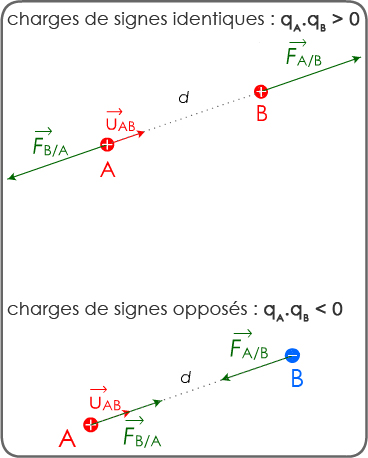
👉 qA.qB > 0 👉 l'interaction est répulsive (doc 2) ;
👉 qA.qB < 0 👉 l'interaction est attractive (doc 2) ;
doc 2. modélisation de l'interaction
électrostatique par des forces
Exercice : Dans un cristal de chlorure de sodium (NaCl), le plus proche voisin d'un ion sodium Na+ est un ion chlorure Cl-. La distance qui sépare leurs centres est d’environ d = 2,82.10-10 m.
1. Déterminer la valeur de la force d’interaction électrostatique entre un ion sodium et un ion chlorure voisin.
2. Indiquer si cette force est attractive ou répulsive.
Données :
Charge élémentaire : e = 1,60.10-19 C
Constante de Coulomb : k = 9,0.109 N.m2.C-2
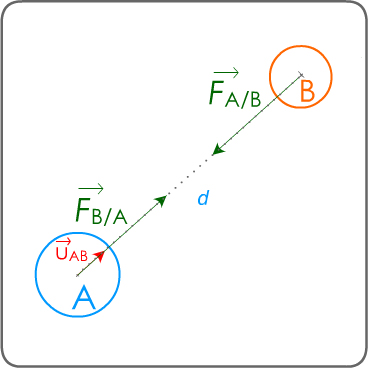
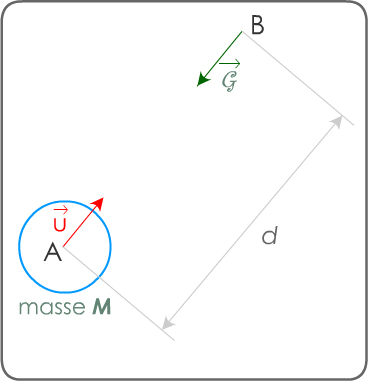
Loi d’interaction gravitationnelle. Soient deux corps sphériques modélisés par leurs centres A et B distants de d (doc 3). A, masse ponctuelle mA exerce sur B, de masse mB, une force :
\( \displaystyle\mathsf {\overrightarrow{F}_{_{A/B}}\ =-\ G\ \frac{m_A.m_B}{d^2}\ \overrightarrow{u}_AB} \)
\( \displaystyle\mathsf {F\ (N)} \)
\( \displaystyle\mathsf {m\ (kg)} \)
\( \displaystyle\mathsf {d\ (m)} \)
\( \displaystyle\mathsf {G\ =\ 6,67.10^{-11}\ N.m^2.kg^{-2}} \)
La 3e loi de Newton donne : \( \displaystyle\mathsf {\overrightarrow{F}_{_{A/B}}\ =-\ \overrightarrow{F}_{_{B/A}}} \)
Une masse n'a pas de signe 👉 mA.mB > 0 👉 l'interaction est toujours attractive.
doc 3. modélisation de l'interaction
gravitationnelle par des forces
3.1. Champ électrostatique \( \displaystyle\mathsf {\overrightarrow{E}} \)
Une charge Q exerce une force sur une charge q 👉 \( \displaystyle\mathsf {\overrightarrow{F}\ =\color{Cerulean}\ k\ \frac{Q.{\color{red}q}}{d^2}\ \overrightarrow{u}} \)
La partie bleue dépend de la charge "source" Q à la distance d.
La partie rouge dépend de la charge "témoin" q.
La force peut s'écrire 👉 \( \displaystyle\mathsf {\overrightarrow{F}\ ={\color{red}q}\color{Cerulean}\ \overrightarrow{E}} \)
avec \( \displaystyle\mathsf {\color{Cerulean}\overrightarrow{E}\ =\ k\ \frac{Q}{d^2}\ \overrightarrow{u}} \)
Un objet chargé modifie les propriétés locales de l'espace :
En un point M, un objet chargé crée une influence, le champ \( \displaystyle\mathsf {\overrightarrow{E_M}} \), pouvant affecter une autre charge q qui, dès lors, subirait la force :
\( \displaystyle\mathsf {\overrightarrow{F}\ =\ q.\overrightarrow{E_M}} \)
\( \displaystyle\mathsf {F\ (N)} \)
\( \displaystyle\mathsf {q\ en\ coulomb\ (C)} \)
\( \displaystyle\mathsf {E\ (N.C^{-1}\ ou\ V.m^{-1})} \)
Considérons l'expression \( \displaystyle\mathsf {\overrightarrow{E}\ =\ k\ \frac{\color{Cerulean}Q}{d^2}\ \overrightarrow{u}} \). Elle dit que si la charge source...
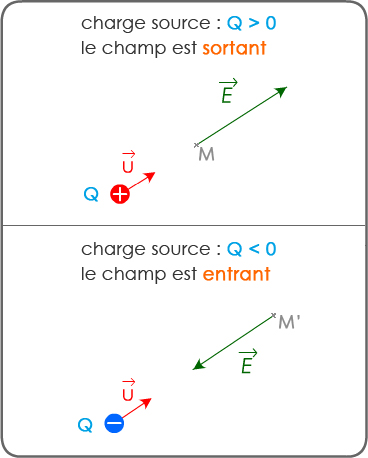
👉 ...Q > 0 👉 le champ \( \displaystyle\mathsf {\overrightarrow{E}} \) est "sortant" (doc 4) ;
👉 ...Q < 0 👉 le champ \( \displaystyle\mathsf {\overrightarrow{E}} \) est "entrant" (doc 4) ;
doc. 4 vecteur champ électrostatique
créé par Q à une distance d
3.2. Champ de gravitation \( \displaystyle\mathsf {\overrightarrow{𝒢}} \)
Un corps "ponctuel" de masse M exerce une force sur une masse m 👉 \( \displaystyle\mathsf {\overrightarrow{F}\ =\color{Cerulean}-\ G\ \frac{M.{\color{red}m}}{d^2}\ \overrightarrow{u}} \)
La partie bleue dépend de la masse "source" M à la distance d de son centre.
La partie rouge dépend de la masse "témoin" m.
La force peut s'écrire 👉 \( \displaystyle\mathsf {\overrightarrow{F}\ ={\color{red}m}\color{Cerulean}\ \overrightarrow{𝒢}} \)
avec \( \displaystyle\mathsf {\color{Cerulean}\overrightarrow{𝒢}\ =-\ G\ \frac{M}{d^2}\ \overrightarrow{u}} \)
Un objet sphérique de masse M modifie les propriétés locales de l'espace :
En un point B, un corps ponctuel de masse M crée une influence, le champ \( \displaystyle\mathsf {\overrightarrow{𝒢_B}} \), pouvant affecter un autre objet de masse m qui, dès lors, subirait la force :
\( \displaystyle\mathsf {\overrightarrow{F}\ =\ m.\overrightarrow{𝒢_B}} \)
\( \displaystyle\mathsf {F\ (N)} \)
\( \displaystyle\mathsf {m\ (kg)} \)
\( \displaystyle\mathsf {𝒢\ (N.kg^{-1}\ ou\ m.s^{-2})} \)
Considérons l'expression \( \displaystyle\mathsf {\overrightarrow{𝒢}\ =-\ G\ \frac{M}{d^2}\ \overrightarrow{u}} \). Elle dit que ...
👉 ... le champ \( \displaystyle\mathsf {\overrightarrow{𝒢}} \) est toujours "entrant" (doc 5) ;
doc. 5 vecteur champ de gravitation \( \displaystyle\mathsf {\overrightarrow{𝒢}} \)
créé par une masse à une distance d
3.3. Lignes de champ
Les lignes de champ sont des courbes imaginaires qui représentent la direction du champ en chaque point de l’espace.
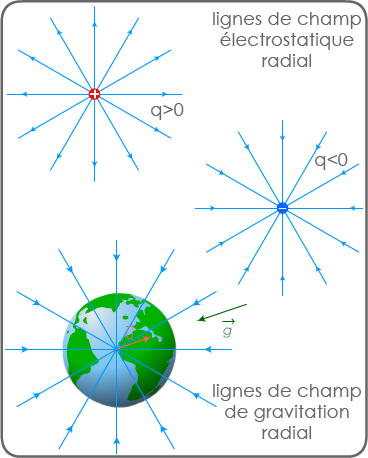
Pour une particule, les lignes sont sécantes en son centre (doc 6)
Pour un astre sphérique, les lignes sont aussi sécantes au centre (doc 6)
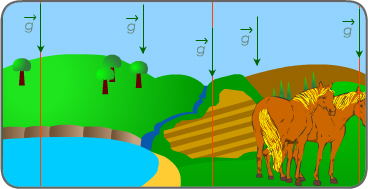
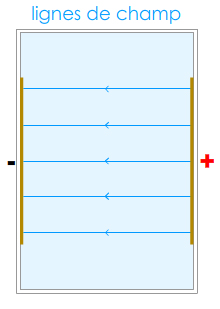
Dans un espace réduit, un champ de gravitation peut être considéré comme uniforme, et les lignes de champ, donc, parallèles (doc 7).
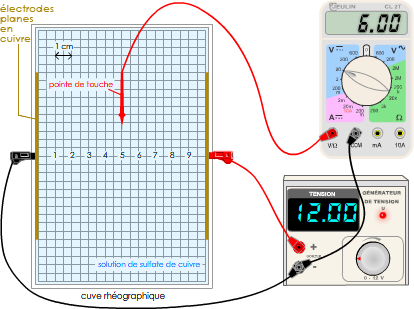
Entre deux plaques parallèles connectées à un générateur de tension continue, un champ électrostatique uniforme peut être cartographié grâce à la cuve rhéographique ↓↓↓
doc. 6 lignes de champ radial
électrostatique et gravitationnel
doc. 7 lignes d'un champ uniforme
de gravitation (espace réduit)