
Rappel :
EXEMPLE DE LA CHUTE LIBRE À DEUX DIMENSIONS :
La trajectoire est une parabole.
Entre les instants t et t + Δt, le vecteur vitesse passe de \( \displaystyle\mathsf {\overrightarrow {v}} \) à \( \displaystyle\mathsf {\overrightarrow {v'}} \).
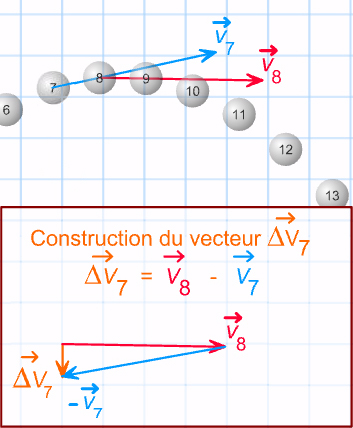
Le vecteur "variation de vitesse à la date t " : \( \displaystyle\mathsf {\overrightarrow {Δv}} \) = \( \displaystyle\mathsf {\overrightarrow {v'}} \) - \( \displaystyle\mathsf {\overrightarrow {v}} \)Entre deux positions successives M et M', à des instants voisins séparés de Δt, on définit le vecteur variation de vitesse \( \displaystyle\mathsf {\overrightarrow{Δv}_{(t)}} \) du point M tel que :
\( \displaystyle\mathsf {\overrightarrow {Δv}\ =\ \overrightarrow {v'}\ - \overrightarrow {v}}\)
Méthode : Construction de Δv 7
1. construction de v 7
2. construction de v 8
3. origine de v 8 sur M7
4. construction de -v 7 à l'extrémité de v 8
5. construction de Δv 7
doc 1. vecteur variation de vitesse
ex. : construction de Δv 7
Les expressions "somme des forces", "force totale", "résultante" sont équivalentes.
Le vecteur peut être ∑F, ∑ F, Fext, Ftot, Frés
Pour étudier le mouvement d'un système soumis à plusieurs forces, on considère qu'il se comporte comme s’il ne subissait qu’une force unique.
On construit la somme des forces, en additionnant les vecteurs forces qui s’appliquent au système.
\( \displaystyle\mathsf {\overrightarrow {∑F}\ =\ \overrightarrow {F_1}\ + \overrightarrow {F_2}\ + \overrightarrow {F_3}\ + \overrightarrow {F_4}...}\)
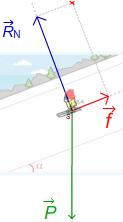
f + RN = - P
ΣF = 0
P + R = 0
ΣF = F

pendule (sans frottement)
ΣF = P + F
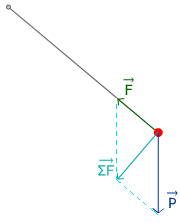
doc 2. le système est soumis au seul poids
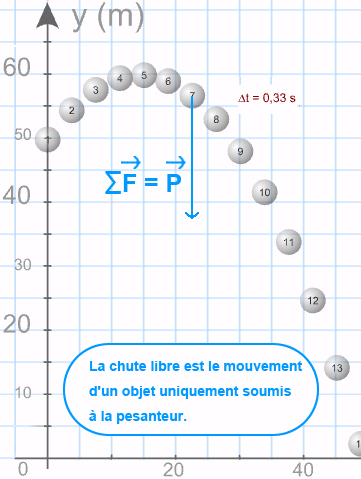
mouvement de la chute libre : ΣF = P
Il s'agit d'une approche de la 2e loi de Newton.
Une relation approchée existe entre ΣF, la somme des forces exercées sur un système de masse m, et son vecteur variation de vitesse Δv(t) entre les dates t et t + Δt :
\( \displaystyle\mathsf {\overrightarrow {∑F}\ =\ m \frac{\overrightarrow {Δv}}{Δt}}\)
\( \displaystyle\mathsf {\overrightarrow {||∑F||}\ en\ N}\)
\( \displaystyle\mathsf {\ m\ en\ kg}\)
\( \displaystyle\mathsf {\overrightarrow {||Δv||}\ en\ m.s^{-1}}\)
\( \displaystyle\mathsf {\ Δt\ en\ s}\)
Exemples : ΣF = k.Δv
CHUTE LIBRE
ΣF = P
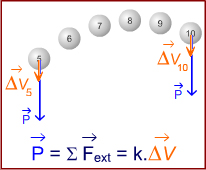
MOVt RECt Ut ACCÉLÉRÉ
ΣF = F
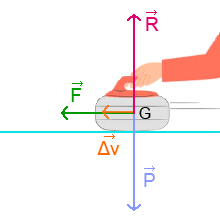
MOVt RECt Ut RALENTI
ΣF = f
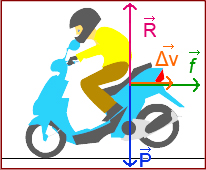
doc 3. ΣF et Δv colinéaires
animation interactive
Remarque 👉 Les vecteurs ΣF et Δv ont même sens. La grandeur m/Δt est positive. 😊
⚠️ Dans le cas très particulier d'une force résultante constante en valeur et direction, la formule ΣF = m·|Δv|/Δt est possible.
Exercice sur le rôle de la masse : Un train régional quitte la gare.
Sa masse est de 180 tonnes (1 tonne = 1000 kg).
Il atteint la vitesse de 72 km/h en 40 secondes, sur une voie horizontale. On néglige les frottements.
1. Calculer la valeur de la force exercée par les moteurs pendant cette phase d'accélération.
2. Une rame est ajoutée, portant la masse totale à m' = 240 tonnes.
Avec la même force, combien de temps met le train pour atteindre 72 km/h ?