
Cette page est la correction d'une évaluation. Voir le sujet à imprimer
EXERCICE 1 : Le VRAI - FAUX
On connait la vitesse moyenne v et la durée t du parcours. On peut écrire \( \displaystyle\mathsf {d = \frac{v}{t}} \)
On peut être immobile et en mouvement en même temps
100 m en 10 s. Cela fait une vitesse moyenne de 36 km/h
La vitesse instantanée d’un mobile est caractérisée par sa direction, son poids et sa densité
EXERCICE 2 : Compléter le tableau suivant :
| Vitesse moyenne v (m/s) | Distance d (m) | Durée t (s) | |
\( \displaystyle\mathsf {v = \frac{d}{t}=\frac{50}{10}}= \) 5 m/s |
50 | 10 | ? |
| 144 | d = v x t = 144 x 20 = 2880 m |
20 | ? |
| 5 | 150 | \( \displaystyle\mathsf {t = \frac{d}{v}=\frac{150}{5}}= \) 30 s |
? |
EXERCICE 3 : Cette chronophotographie a été réalisée avec des intervalles entre deux clichés de Δ t = 0,25 s.

a) Qualifier ce mouvement : Réponse
Les distances parcourues diminuent. Il s'agit d'un Mouvement Rectigne Ralenti
b) Calculer la vitesse moyenne du scooter sur cette distance de 65 m : Réponse
Nous comptons 13 intervalles.
\( \displaystyle\mathsf {vitesse\ moyenne = \frac{distance\ totale}{temps}=\frac{65}{(13\ x\ 0,25)}=\frac{65}{3,25}} \)
v = 20 m/s
c) Exprimer cette vitesse moyenne en km/h : Réponse
20 x 3,6 = 72
v = 72 km/h
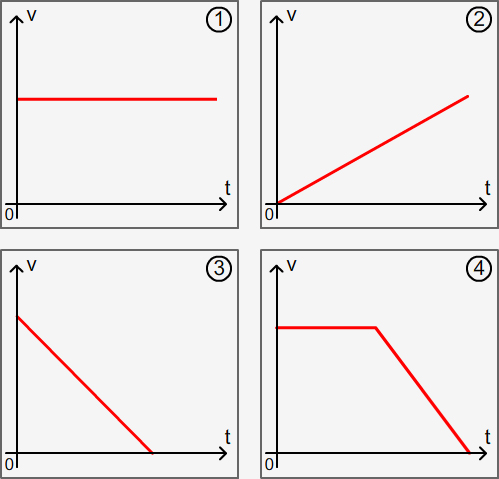
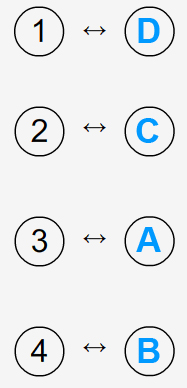
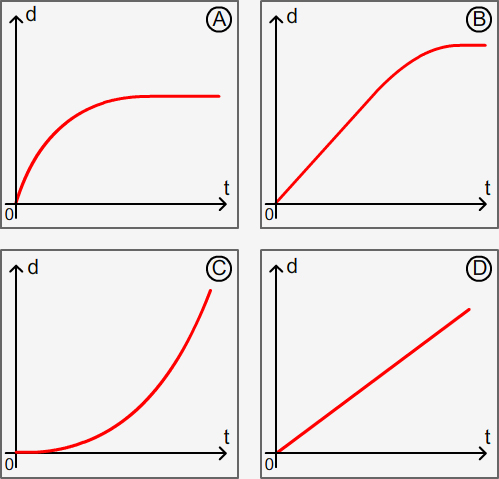
EXERCICE 4 : Relier chaque diagramme de gauche (1, 2, 3 ou 4) au diagramme de droite (A, B, C ou D) correspondant :
 |
Réponse
 |
 |