
Pour étudier un mouvement, il faudra définir le système et le référentiel.
1.1. Système
Le système est l'objetun solide dont on étudie le mouvement.
Si l'objet est en translationDéplacement d'un solide de telle façon que tous ses points décrivent des trajectoires identiques entre elles, tous les points ont des trajectoires identiques. Décalées, mais identiques. Mais tous les points de l'objet pourraient avoir des mouvements différents. Pour simplifier, on modélise alors l'objet par un point qui aurait la masse de l'objet : le point matérielOn appelle point matériel ou masse ponctuelle un système mécanique qu'il est possible de modéliser par un point M auquel est associée sa masse m.
1.2. Référentiel
Le professeur demande aux élèves assis :
- Sauriez-vous décrire votre mouvement ? Position, vitesse, trajectoire...
- Monsieur, nous sommes immobiles.
- Mais la Terre tourne, rétorque l'enseignant.
- Monsieur, nous sommes immobiles p/r à la Terre.
- Pas mal ! le référentiel est donc la Terre. Et pour la position ?
- On pourrait mesurer à partir du coin, là-bas.
- Parfait. Tu as déjà l'origine du repère qu'il faudra choisir.
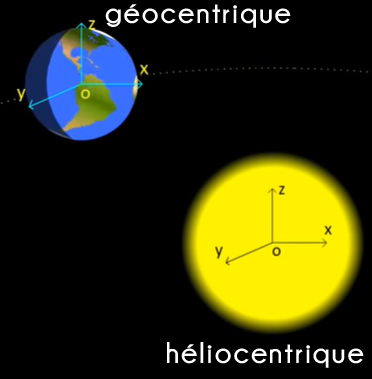
Le référentiel est l'objet par rapport auquel on étudie le mouvement.
On lui associe un repère d'espace et un repère de temps.
On choisit le référentiel en fonction du système étudié.
1.3. Relativité du mouvement
La description du mouvement dépend du référentiel choisi.
Exemple : La trajectoire d'une balle lâchée dans un train n'est pas la même pour un observateur se trouvant dans le train (le train est le référentiel) et pour un autre observateur se trouvant sur le sol (le référentiel est la Terre).


La trajectoire est la courbe formée par les positions successives d'un point matériel.

Entre les instants t et t + Δt, le mobile se déplace de M en M' en suivant un vecteur déplacement \( \displaystyle\mathsf {\overrightarrow {MM'}} \) dont les caractéristiques sont :
- direction : selon la droite (MM') ;
- sens : de M vers M' ;
- valeur : la longueur du segment [MM'].
Vocabulaire : le mouvement est...
rectiligne : la trajectoire est une droite
circulaire : la trajectoire est un cercle
curviligne : la trajectoire est une courbe
Entre deux positions successives, notées M et M', à des instants voisins séparés de Δt, on définit le vecteur vitesse \( \displaystyle\mathsf {\overrightarrow {v_M}} \), du point M tel que :
\( \displaystyle\mathsf {\overrightarrow {v_M}\ =\ \frac{\overrightarrow {MM'}}{Δt}} \)
Les caractéristiques du vecteur vitesse du point M sont :
- direction : celle du segment [MM'] ;
- sens : celui du mouvement ;
- valeur : proportionnelle, selon l'échelle, à la valeur de la vitesse \( \displaystyle\mathsf {\ {v_M}\ =\ \frac{MM'}{Δt}} \) (en m.s-1).
EXEMPLE DU MOUVEMENT RECTILIGNE UNIFORME :

EXEMPLE DU MOUVEMENT RECTILIGNE UNIFORMÉMENT ACCÉLÉRÉ :

EXEMPLE DE LA CHUTE LIBRE À UNE DIMENSION :
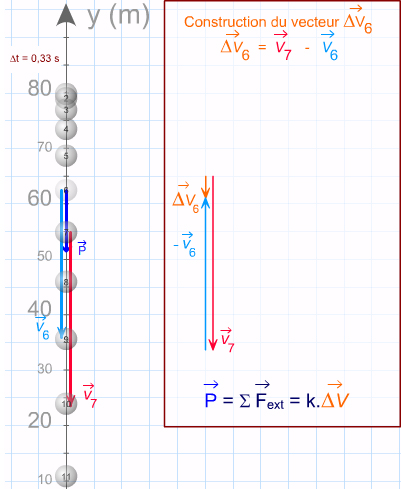
La trajectoire est une droite verticale.
Entre les instants t et t + Δt, le vecteur vitesse passe de \( \displaystyle\mathsf {\overrightarrow {v}} \) à \( \displaystyle\mathsf {\overrightarrow {v'}} \).
\( \displaystyle\mathsf {\overrightarrow {Δv}} \) = \( \displaystyle\mathsf {\overrightarrow {v'}} \) - \( \displaystyle\mathsf {\overrightarrow {v}} \)
EXEMPLE DE LA CHUTE LIBRE À DEUX DIMENSIONS :
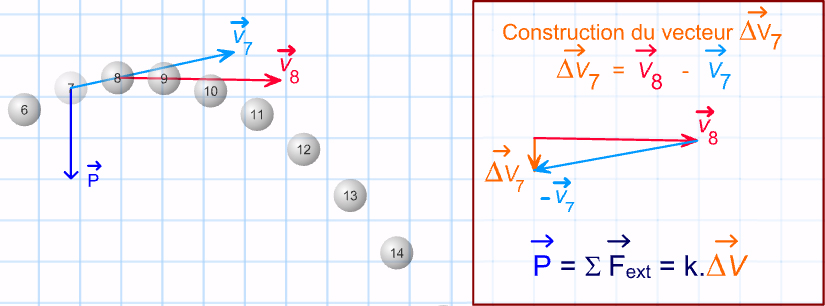
La trajectoire est une parabole.
Entre les instants t et t + Δt, le vecteur vitesse passe de \( \displaystyle\mathsf {\overrightarrow {v}} \) à \( \displaystyle\mathsf {\overrightarrow {v'}} \).
\( \displaystyle\mathsf {\overrightarrow {Δv}} \) = \( \displaystyle\mathsf {\overrightarrow {v'}} \) - \( \displaystyle\mathsf {\overrightarrow {v}} \)
Entre deux positions successives, notées M et M', à des instants voisins séparés de Δt, on définit le vecteur variation de vitesse \( \displaystyle\mathsf {\overrightarrow {Δv}} \), du point M tel que :
\( \displaystyle\mathsf {\overrightarrow {Δv}\ =\overrightarrow {v'}\ - \overrightarrow {v}}\)
Le vecteur variation de vitesse instantanée \( \displaystyle\mathsf {\overrightarrow {Δv}} \) a même direction et même sens que la somme des forces extérieures \( \displaystyle\mathsf {\overrightarrow {{ΣF}_{ext}}}\) appliquées au système ; le seul poids dans le cas de la chute libre.
\( \displaystyle\mathsf {\overrightarrow {P}\ = Σ\overrightarrow {F_{ext}}\ = k.\overrightarrow {Δv}}\)