
Si les forces qui s'exercent sur un système se compensent, ce système est soit immobile soit en mouvement rectiligne uniforme. La réciproque est vraie.
\( \displaystyle\mathsf {\sum\overrightarrow{F}_{ext}\ =\overrightarrow{0}\ {\color{red} ⇔}\ \overrightarrow{v}_G\ =\ \overrightarrow{0}\ ou\ \overrightarrow{v}_G\ ne\ varie\ pas} \)
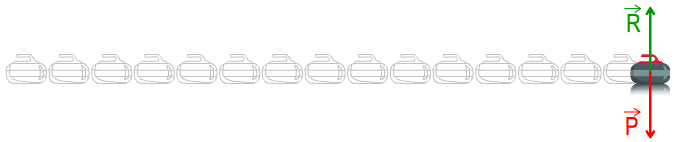
Lorsqu'un système est soumis à des forces qui se compensent, sa vitesse n'est pas modifiée.

Ici, le poids du cône
en papier et les
frottements de l'air
se compensent,
comme pour le
parachute.
Comme le principe d'inertie, sa contraposéela contraposée du principe d'inertie s'obtient en prenant la négation des deux propositions ne s'applique que dans les référentiels galiléensRéférentiel dans lequel le principe d'inertie est vérifié. Le référentiel terrestre sera considéré comme galiléen
Si un système est soumis à des forces qui ne se compensent pas, sa vitesse varie. La réciproque est vraie.
\( \displaystyle\mathsf {\sum\overrightarrow{F}_{ext}\ ≠\overrightarrow{0}\ {\color{red} ⇔}\ \overrightarrow{v}_G\ varie} \)
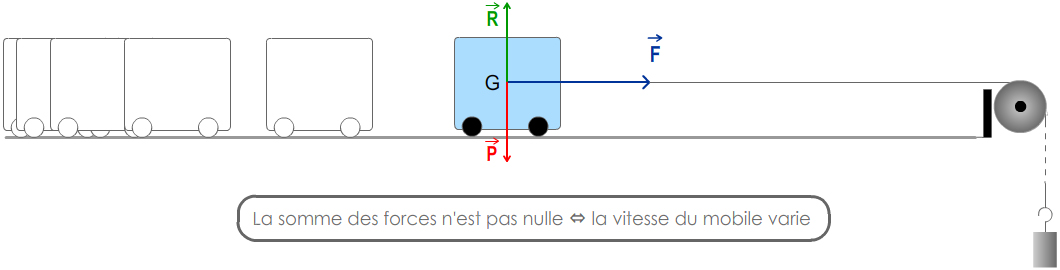
Un système est en chute libre (référentiel terrestre) lorsqu'il n'est soumis qu'à son poids :
\( \displaystyle\mathsf {\sum\overrightarrow{F}_{ext}\ =\overrightarrow{P}} \)
