Cette page est la correction d'une évaluation. Voir le sujet à imprimer
EXERCICE 1 : Le VRAI - FAUX
La formule qui donne la masse volumique est \( \displaystyle\mathsf {\rho = \frac{m}{V}} \)
On peut trouver la masse volumique d’un liquide avec une balance et un thermomètre
Pour une essence ρ = 0,69 g/mL. La masse d’un litre sera de 69 g
La masse d’une substance est proportionnelle à son volume
EXERCICE 2 : Compléter le tableau
| masse (g) | volume (mL) | masse volumique (g/mL) | |
| 20 | 25 | 0,8 |
? |
| 270 | 20 |
13,5 | ? |
100 |
80 | 1,25 | ? |
EXERCICE 3 : La balance a été tarée avant de recevoir un liquide.
a) Quelle est la masse volumique de ce liquide ? Justifier par le calcul.
Réponse
\( \displaystyle\mathsf {\rho = \frac{m}{V}\ = \frac{79,0}{100} = 0,790\ g/mL} \)
ρ = 0,790 g / mL
b) Exprimer cette masse volumique en kg / L :
Réponse
\( \displaystyle\mathsf {\rho = \frac{m}{V} = \frac{\frac{79,0}{1000}} { \frac{100}{1000}} = \frac{79,0}{1000} × \frac{1000}{100} = 0,790\ kg/L} \)
ρ = 0,790 kg / L

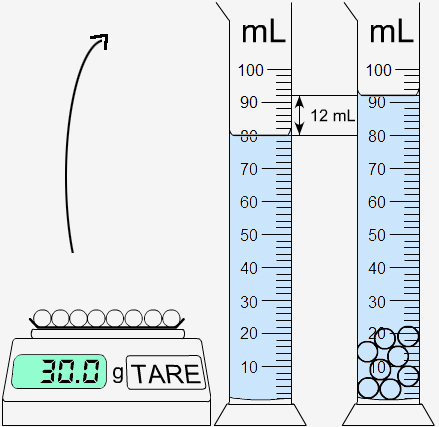
EXERCICE 4 : On pèse des billes en verre avant de les plonger dans 80 mL d’eau. Le niveau de l’eau monte à 92 mL.
a) Quelle est la masse volumique de ce verre ? Justifier par le calcul.
Réponse
\( \displaystyle\mathsf {\rho = \frac{m}{V}\ = \frac{30,0}{12} = 2,5\ g/mL} \)
ρ = 2,5 g / mL
b) Exprimer cette masse volumique en kg / m3 :
Réponse
\( \displaystyle\mathsf {\rho = \frac{m}{V} = \frac{\frac{30,0}{1000}} { \frac{12}{1 000 000}} = \frac{30,0}{1000} × \frac{1 000 000}{12} = 2500\ kg/m^3} \)
ρ = 2500 kg / m3